@Julie Kallini等：《Mission Impossible Language Models》

摘要

• 针对Chomsky提出的观点——大型语言模型（LLMs）能够同样有效地学习人类可能和不可能的语言——进行了实验验证。
• 通过设计一系列基于英语数据的合成“不可能语言”，作者评估了GPT-2小型模型的学习能力。
• 核心发现：GPT-2在学习不可能语言时相较于英语控制组表现挣扎，挑战了上述观点。
• 研究希望开启一条新的探究路径，测试不同LLM架构在不可能语言上的表现，以深入理解语言学习机制。

引言

• 背景：
  • Chomsky等人（2023）声称LLMs无法区分可能与不可能语言，且这一特性不可改变。
  • Bolhuis等人（2024）进一步认为LLMs能生成不可能语言，甚至优于自然语言。
• 研究现状：
  • 上述观点缺乏充分的实验证据支持，仅引用Mitchell和Bowers（2020）的单一研究。
• 本文目标：
  • 通过实验测试LLMs是否能平等学习可能与不可能语言。
  • 提出不可能语言的复杂性连续统（图1），从随机打乱到基于计数规则的语言。
• 方法：
  • 使用GPT-2小型模型和BabyLM数据集，设计并测试多种不可能语言。

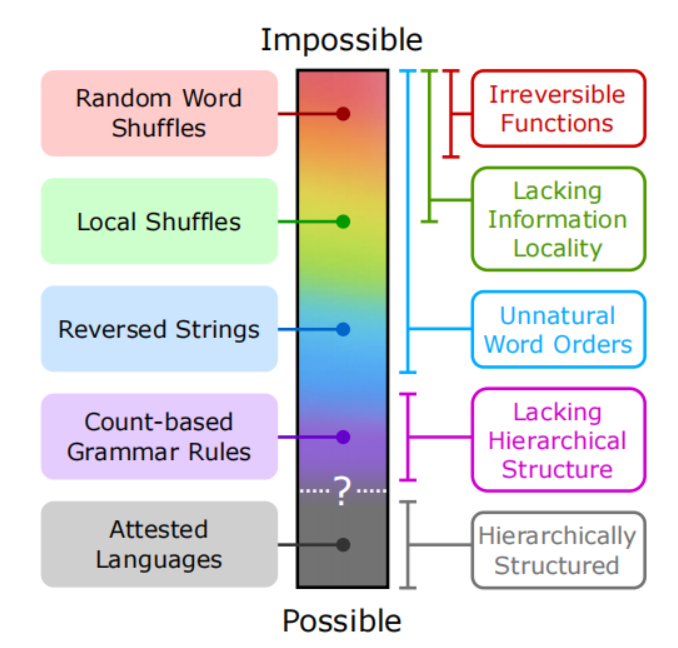
背景和相关工作

2.1 不可能的人类语言与语言共性

• 定义难题：
  • 语言学界对“不可能语言”的定义尚无共识。
  • 递归被认为是人类语言的普遍特性（Chomsky，1957），但存在争议（如Pirahã语言，Everett，2012）。
• 不可能语言的特征：
  • Moro等人（2023）认为不可能语言依赖线性词序而非层级结构。
  • Musso等人（2003）提出基于词位计数的规则作为例子。
  • 区分：“不可能的”语言 vs. “类型学上标记的”语言（较为罕见或不常见的语言特征）

2.2 用非自然词序训练语言模型

• 已有研究：
  • Mitchell和Bowers（2020）发现RNN能学习倒序英语。
  • Transformer模型对词序和短语结构敏感（Alleman等人，2021）。

2.3 语言模型与形式语言

• Chomsky层级：
  • 人类语言被认为比上下文无关语言稍微更具表现力（Shieber，1985）。
    • 上下文无关语言（CFLs）
    • 人类语言因其交叉序列依赖等特性，比上下文无关语言更具表达力，被归为轻度上下文敏感语言。
  • RNNs能有效建模CFLs，如计数语言和DYCK语言，展现了处理层次结构的能力。
  • Transformers理论上图灵完备，但在实践中难以处理正则语言和CFLs，却在自然语言任务上表现出色。
    • 这个悖论表明，要么人类语言的复杂性被高估，要么Transformers需要增强（如添加栈或结构化训练）以更好地捕捉嵌套结构。

不可能语言

作者定义了三种类型的合成不可能语言，基于对英语数据的系统性修改：

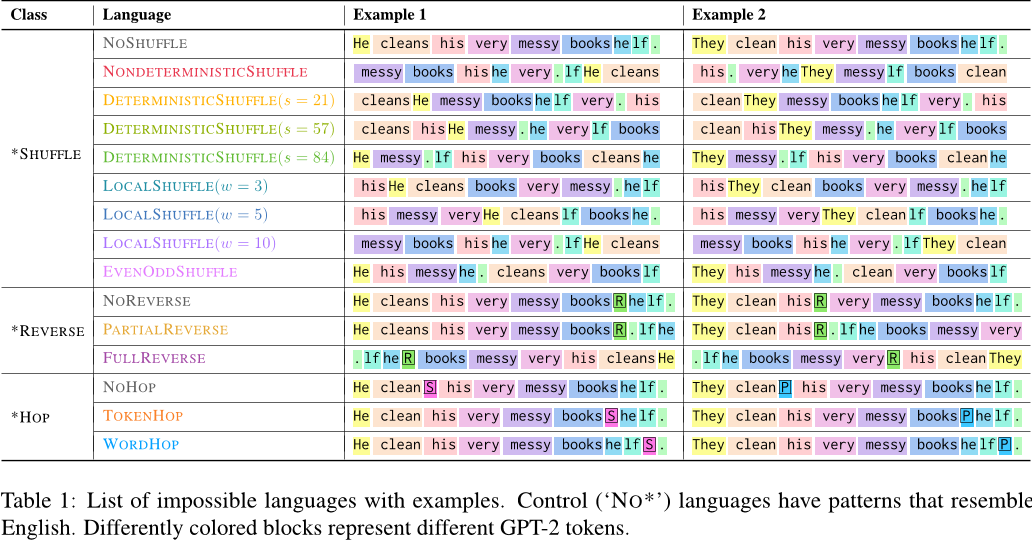
• *SHUFFLE：
  • NoShuffle
    这是控制组，句子保持原始英语词序。在随机位置插入一个标记 token
  • NonDeterministicShuffle
    句子的词序被完全随机打乱，标记 token 位置不变。
  • DeterministicShuffle
    打乱方式基于句子长度，对于相同长度的句子，词序重排模式固定。例如，所有五个词的句子都按同一模式打乱。
  • LocalShuffle
    仅在固定窗口内（如每 3 个词）打乱词序。
  • EvenOddShuffle
    有偶数索引的标记首先出现，然后是所有奇数索引的标记。
• *REVERSE：
  • NoReverse
    控制组，句子保持原始英语词序。仅插入标记 token。
  • PartialReverse
    在标记 token 之后的部分句子被反转。
  • FullReverse
    整个句子（包括标记 token）被完全反转。
• *HOP：
  • NoHop
    控制组，动词被词干化，标记 token 紧跟在动词后。例如，“He cleans the room”变为“He clean [S] the room”（[S] 表示单数）。这接近自然英语的简化形式。
  • TokenHop
    标记 token 被放置在动词后 4 个 token 的位置。
  • WordHop
    标记 token 被放置在动词后 4 个单词的位置，跳过标点。

实验

实验1：语言模型反映不可能连续统

• 目的：
  测试GPT-2模型在学习自然语言和不同类型不可能语言时的效率，验证其是否对自然语言有偏好。
• 方法：
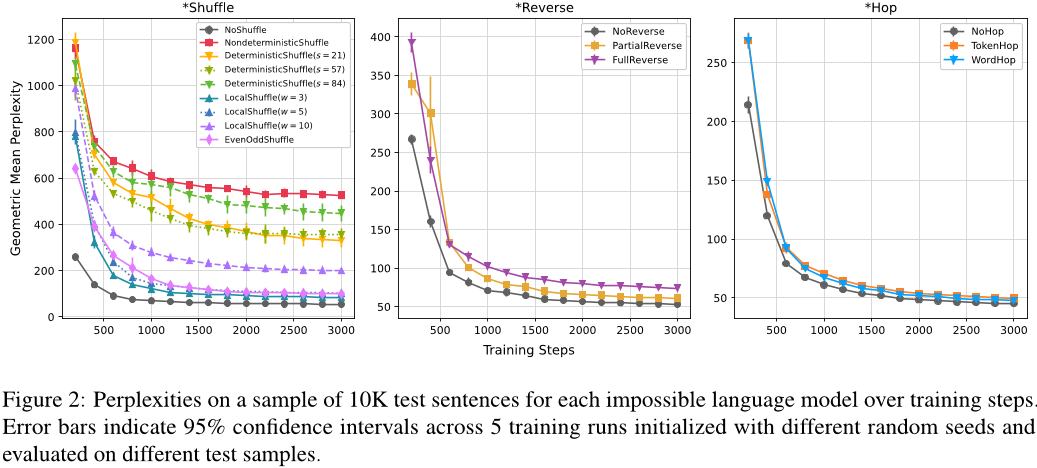
  使用困惑度（perplexity） 作为评估指标。困惑度越低，说明模型对语言的预测越准确。实验比较了模型在自然语言（如英语）和不可能语言（如*\SHUFFLE、*REVERSE、*HOP）上的表现。
• 结果：
  • 自然语言的困惑度最低，模型学习效果最好。
  • 不可能语言中，*SHUFFLE（随机打乱词序）的困惑度最高，*REVERSE和*HOP的困惑度介于两者之间。
  • 不同不可能语言的困惑度差异反映了其结构复杂性和不自然程度。
• 意义：
  表明GPT-2模型更擅长学习自然语言，对不可能语言的掌握能力较弱。

实验2：语言模型不喜欢计数规则

• 目的：
  深入研究模型对*HOP语言中基于计数规则的语法结构的预测能力。
• 背景：
  *HOP语言的特点是将动词的单复数标记放置在动词后固定的token或单词位置，这种基于计数的规则在自然语言中不常见。
• 方法：
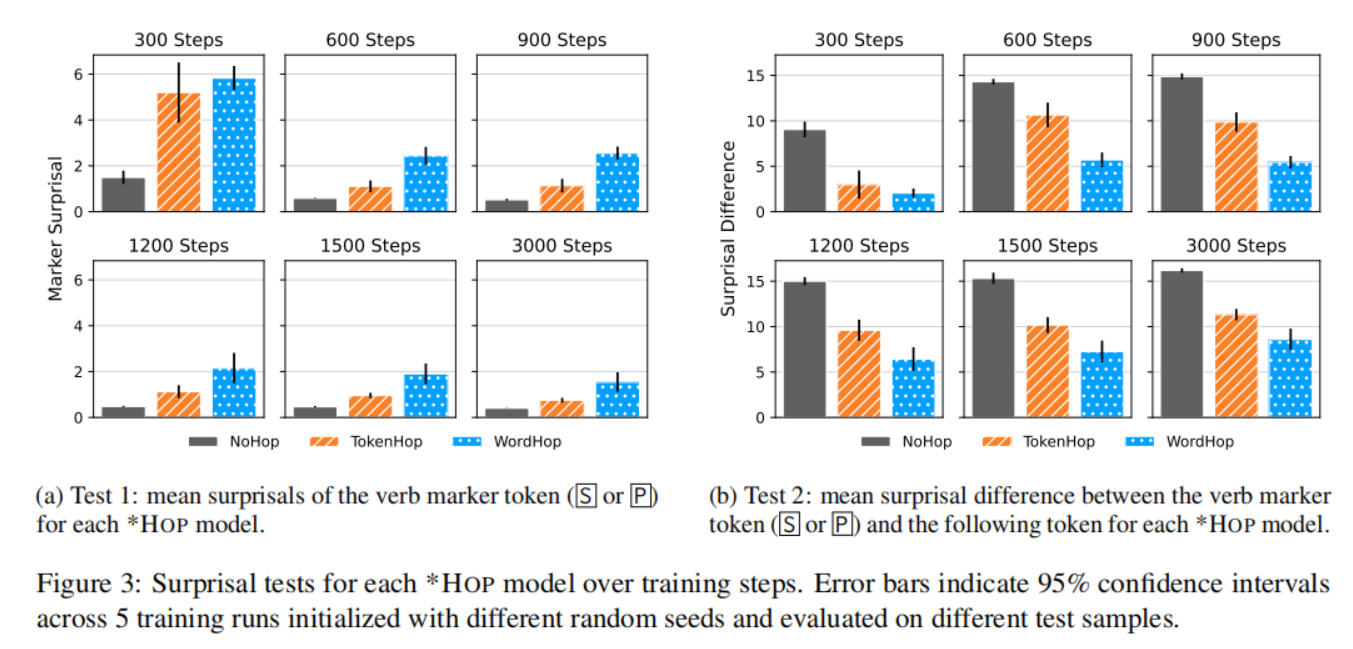
  使用惊异值（surprisal） 衡量模型对标记位置的预测准确性。惊异值越低，说明模型对该位置的预测越“期待”。实验对比了自然语言类似的NoHop和基于计数的TokenHop、WordHop。
  • $S(w_i)=-{\log }_{2}p(w_i|w_1,\dots ,w_{i-1})$
  • 测试1：标记token的平均惊异值
  • 测试2：最小对中的惊异值差异：通过比较标记 token 和其后 token 的惊异值差异，评估模型对标记 token 的“期待”程度。
    • 最小对：两个句子在结构上几乎一样，唯一的区别是标记 token S的存在与否，因此它们构成了一对“最小对”。
• 结果：
  • 在NoHop（自然语言类似）中，模型对标记位置的预测最准确。
  • 在TokenHop（基于token计数）和WordHop（基于单词计数）中，预测能力较差，尤其是WordHop。
• 意义：
  模型对自然语法结构的掌握优于基于计数的规则，显示出对自然语言的偏好。

实验3：语言模型对不自然模式发展自然解法

• 目的：
  探究GPT-2模型在学习*HOP语言时，内部机制如何适应不自然的语法规则。
• 方法：
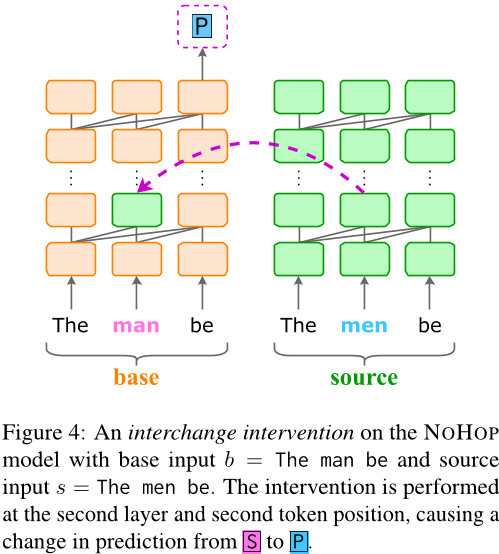
  使用因果抽象分析（causal abstraction analysis），通过干预模型的中间表示，观察其对语法标记预测的影响。例如，交换单数和复数主语的表示，测试模型对标记的响应。
  • 构造两个输入句子
    • base input（基础输入）：一个单数主语的句子，比如“He clean ...”。→ S 单数
    • source input（来源输入）：一个复数主语的句子，比如“They clean ...”。→ P 复数
  • 干预操作
    • 模型在处理句子时，会一层一层地计算，每个层都会生成一些表示（叫“隐藏状态”）。
    • 研究者在某个层、某个单词（token）的位置，把base input的表示替换成source input的表示。
  • 观察结果替换之后，看模型的预测会不会变。他们用一个指标叫交换干预准确率（IIA） 来衡量：干预后，模型预测P的概率是不是比S高。
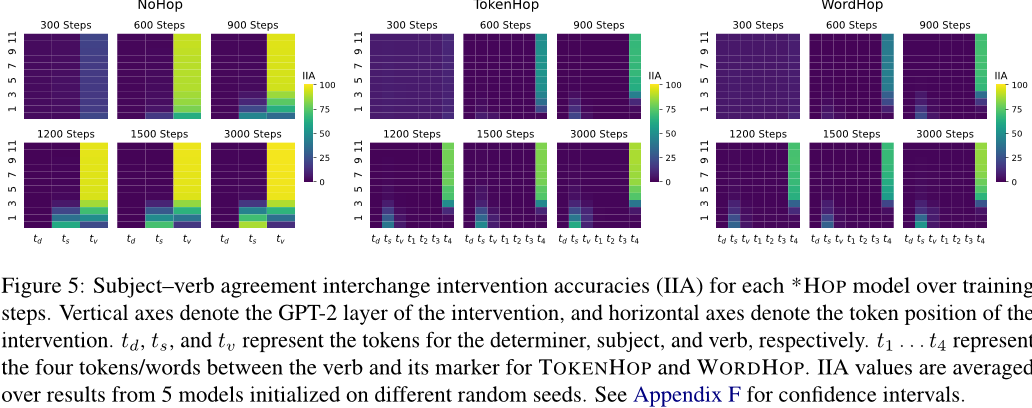
• 结果：
  • 所有*HOP模型都发展出模块化解决方案：早期层处理主语，后期层关注标记位置。
  • 但*NoHop（自然语言类似）的学习效率更高，预测准确率在更少的训练步骤内提升。
• 意义：
  尽管模型能适应不自然规则，但其学习效率和机制发展速度不如自然语言，反映了对自然结构的内在倾向。

讨论和结论

• 实验总结：
  • GPT-2在学习不可能语言时表现挣扎，与学习自然语言相比效率较低。
  • 这一结果挑战了Chomsky等人关于LLMs无法区分可能与不可能语言的观点。
• 意义与展望：
  • 作者认为LLMs可作为研究语言学习的有效工具。
  • 呼吁进一步探索LLMs在区分可能与不可能语言方面的潜力及其局限性。